Using
R as a calculator
R
can be used as a powerful calculator by entering equations directly at
the prompt in the command console. Simply type your arithmetic
expression and press ENTER. R will evaluate the
expressions and respond with the result. While this is a simple
interaction interface, there could be problems if you are not careful. R
will normally execute your arithmetic expression by evaluating each item
from left to right, but some operators have precedence in the order of
evaluation. Let's start with some simple expressions as examples.
Simple
arithmetic expressions
The
operators R uses for basic arithmetic are:
+
Addition
- Subtraction
* Multiplication
/ Division
^ Exponentiation
Let's
experiment with some arithmetic expressions.
4
+ 8 will return the result
12
5 * 14 will return the
result 70
7 / 4 will return the
result 1.75
4 + 5 + 3 will return the result 12
4 ^ 3 will return the
result 64
Operator
precedence
More
complex expressions can cause problems if you are not careful.
4
+ 5 * 3 will return the result 19
Notice
that the expression was not evaluated strictly left to right. R actually
evaluated 5 * 3 and then added that result to 4. The R operator
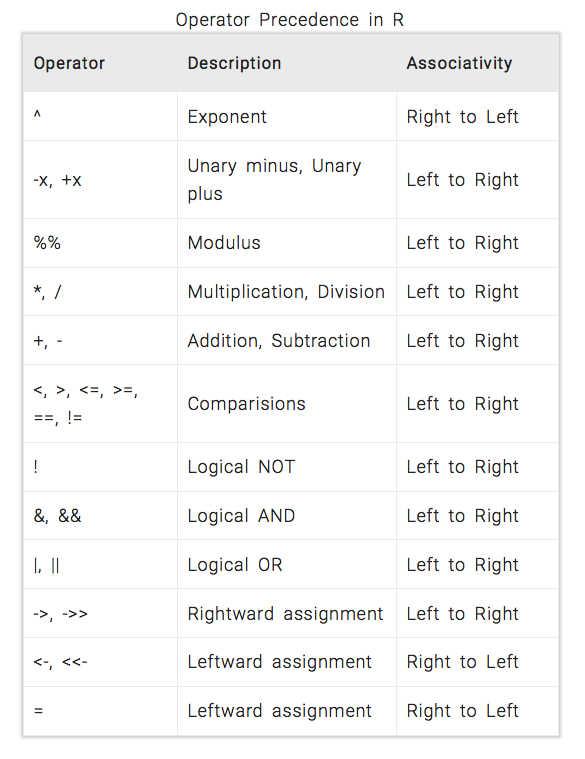
precedence rules caused this result. Figure 1 below shows the various
precedence rules R uses to evaluate expressions. The rules at the top of
the table have highest precedence and are executed first. When operators
have equal precedence, the expression is evaluated left to right.
Figure
1 - Operator Precedence in R
If
you meant to add 4 and 5, then multiply the result by 3, you will need
to add parenthesis to the expression thereby imposing your operation
order on evaluation process. In the case of this example, you could
enter
(4
+ 5) * 3 will return the result 18
Try
another example:
4
+ 3 ^ 2 will return the result 13
While
(4
+ 3) ^ 2 will return the result 49
You
can also compute the root of a value by using fractional powers
4
^ 0.5 will return the
result 2
16 ^ 0.25 will return the result 2
You
can use parenthesis when you want to compute fractional roots that
cannot be expressed as finite decimal numbers
16
^ (1/4) will return the result 2
8
^ (1/3) will return the result 2
As
you can see, it is helpful to use parenthesis to explicitly communicate
the order that you want each operation to be evaluated. When you nest
parenthesis, the arithmetic expression in the innermost parenthesis will
be evaluated first, going left to right by operator precedence. All
other evaluation will move outward from there, again, going left to
right by operator precedence.
Here
is an example of a more complex expression that uses parenthesis to
explicitly control the evaluation process. The original expression
is:
You
will enter this in the RStudio command console:
((435.4
* 3.56) / (34 + 3)^2)^(1/3)
The
result of this expression is: 1.042265
Notice
how you can control the order of evaluation by using parenthesis.
Now
you can accurately carry out most computations from the RStudio command
console.
A
note about computers and computing precision in R
While
R is developed as a portable computing environment, you may discover
that different computers will compute slightly different results for the
same computational steps. In most instances, these differences are small
and are artifacts of the processor in your computer. This behavior is
different than differences caused by errors in your computations. When
this occurs, ensure that all of your computational steps are correct
before proceeding on. Normally, these types of differences will be small
and should not impact your work.
Another
different type of error involves the representational precision in a
computer. In this case, the physical way computers store numbers is the
culprit. Integers [whole numbers] are stored exactly as they are in
computer memory. The various operators manipulate integers precisely.
Decimal [float point] numbers are stored differently. Your computer
stores an approximation of a decimal number rather than the exact value.
For small decimal values, this approximation is very accurate. For
non-finite decimals, like 1/3, the approximation is not exact. While the
error in the approximation is very small, it can, in the right
circumstance, cause computational issues. Here is a simple example that
will demonstrate this behavior.
You
know that
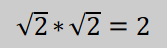
[1]
and
that
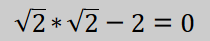
[2]
If
we compute expression [1] in R, we get
2^(1/2)
* 2^(1/2)
2
but
expression [2] will result in
2^(1/2)
* 2^(1/2) - 2
4.440892e-16
This
computational result is the actual difference between expression 2^(1/2)
* 2^(1/2) and the numeric value 2. This difference is very small and it
will normally not impact your computations [this behavior is better than
most top end calculators], but be aware of this precision issue when you
conduct complex calculations.

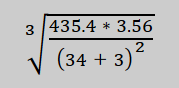
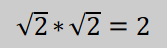 [1]
[1] 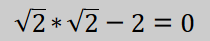 [2]
[2]